↜ Back to index Introduction to Numerical Analysis 1
Part b—Lecture 2
Today we talk more about the numerical scheme for the heat equation that we derived in Lecture b1.
Numerical scheme for the heat equation in Fortran
Here is an example Fortran code for the case a = b = 0 and u_0(x) = \sin(\pi x), M = 10 and \tau = h^2 / 4. The exact solution is expected to be u(x,t) = \exp(-\pi^2 t) \sin(\pi x).
implicit none
! introduce constants M and pi
integer, parameter :: M = 10
real, parameter :: pi = 4. * atan(1.)
integer n, k, nmax
real h, tau, x
! We use arrays to store the values of u_n (in u) and u_{n+1} (in v)
! The arrays will be indexed from 0 to M.
! 👇 M must be a constant to be used here.
real, dimension(0:M) :: u, v
h = 1. / M
tau = h * h / 4.
! 👇 we solve the problem up to time t_nmax = 0.5
nmax = 0.5 / tau
! Initialize u with the initial data u_0 and print the values.
! Since sin(0) = sin(pi) = 0 = a = b, we do not need to set the boundary data
! separately.
do k=0, M
x = k * h
u(k) = sin(pi * x)
end do
! Print the initial data
call printstep(0., u)
do n=0, nmax-1
! One step of the finite difference method from u_n to u_{n+1}
! Array u holds the values of u_n.
! Array v will be filled with computed values of u_{n+1}.
v(0) = u(0) ! boundary condition is constant in time
do k = 1, M-1
v(k) = u(k) + (tau / (h * h)) * (u(k - 1) - 2 * u(k) + u(k + 1))
end do
v(M) = u(M) ! boundary condition is constant in time
! Print the solution
call printstep((n+1) * tau, v)
! store the values of v in u
u = v
end do
contains
! Prints the values of the solution at a given time step
subroutine printstep(tn, un)
real tn
real, dimension(0:M) :: un
integer k
do k = 0, M
print *, tn, k * h, un(k)
end do
! print an empty line (needed for gnuplot)
print *
end subroutine
endThe output consists of values t_n, x_k and u_{n, k}, one (n, k) per line.
0.00000000 0.00000000 0.00000000
0.00000000 0.100000001 0.309017003
0.00000000 0.200000003 0.587785244
0.00000000 0.300000012 0.809017062
0.00000000 0.400000006 0.951056540
0.00000000 0.500000000 1.00000000
0.00000000 0.600000024 0.951056480
0.00000000 0.699999988 0.809017003
0.00000000 0.800000012 0.587785184
0.00000000 0.900000036 0.309016794
0.00000000 1.00000000 -8.74227766E-08
2.50000018E-03 0.00000000 0.00000000
2.50000018E-03 0.100000001 0.301454812
2.50000018E-03 0.200000003 0.573401153
...Plotting the solution
We included an empty line after the data for each time step to allow gnuplot understand that this data is on a regular two dimensional grid. To plot such two dimensional data in gnuplot, we use splot instead of plot.
First we save the output in a file, say sol.txt.
$ ./a.exe > sol.txtThen in gnuplot we can plot the data using the following commands.
set xlabel 't_n'
set ylabel 'x_k'
set zlabel 'u'
splot 'sol.txt'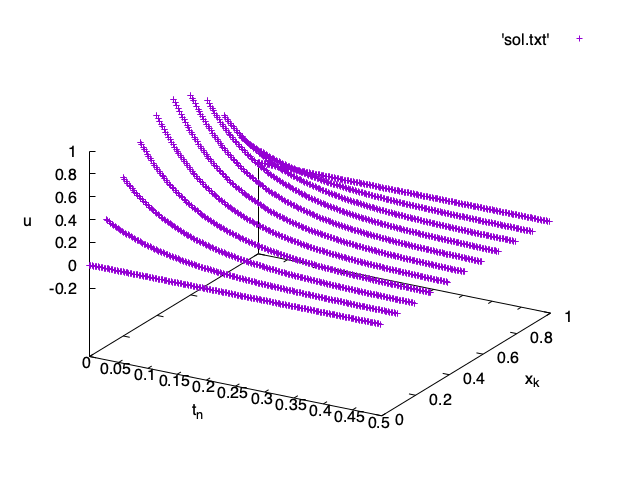
This is a bit difficult to understand, so we usually connect the points of the solution into a mesh that is a bit easier to read, by adding w l to the splot command:
splot 'sol.txt' w lHere w l is a shorthand for with lines.
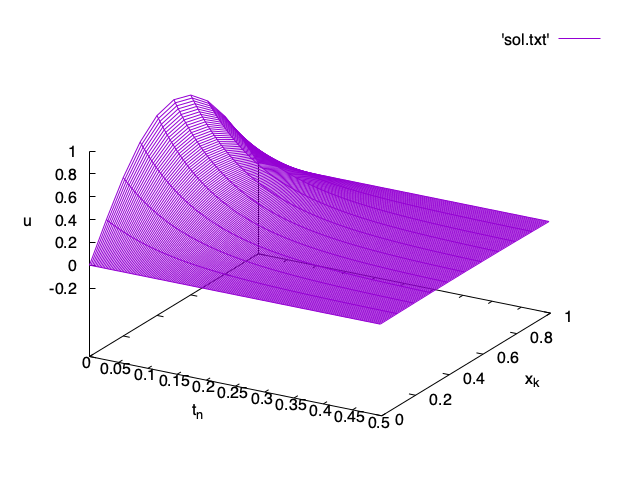
Note how much smaller the time step \tau is compared to the space step h. Unfortunately, with the numerical method discussed here we need to choose \tau \leq \frac{h^2}2. We will discuss this in more detail later. Try to change \tau to h^2 in the program and see what happens to the solution.
Making an animation
However, since the solution depends on time, it is often best to plot the solution as a sequence of graphs of u_{n, k} as a function of x_k, one for each n.
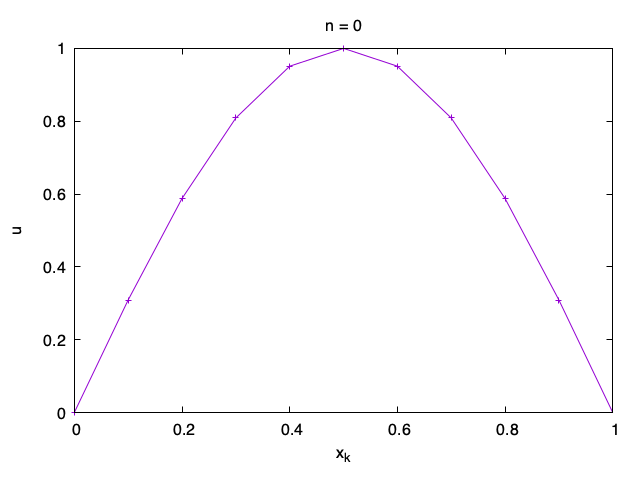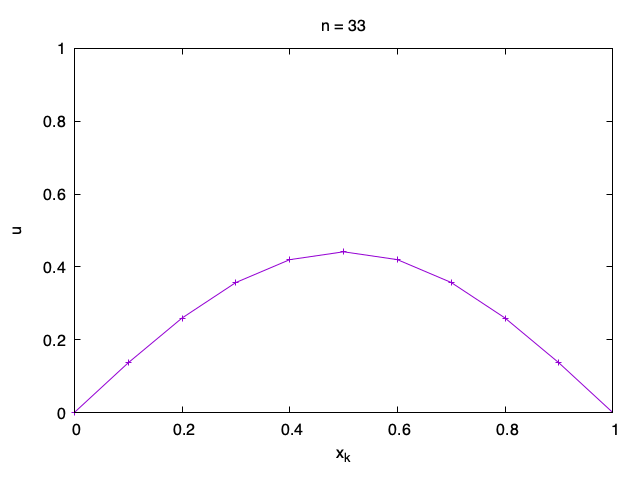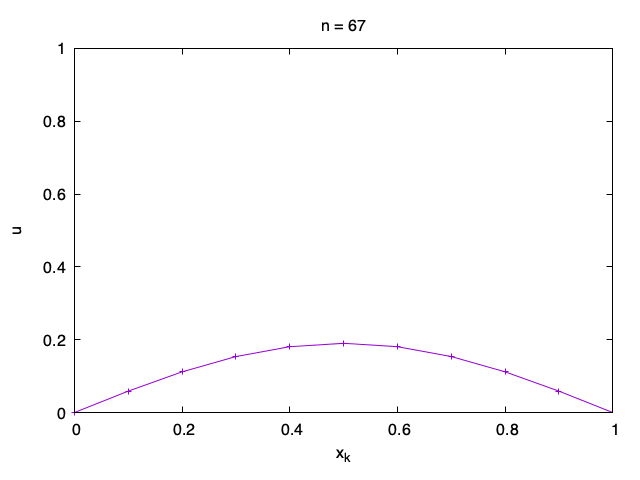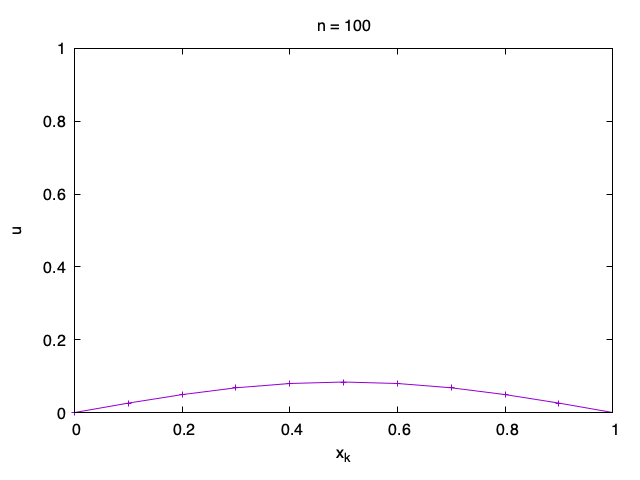
To plot only the graph for one time step as in the animation above, say n=42, you can use the gnuplot commands
plot 'sol.txt' every :::42::42 using 2:3 w linespointsThe command that selects the 42nd time step is every :::42::42. The number of : characters is important. For more on this syntax see How do I plot a part of data in a file ?.
Plotting using a contour plot
Another useful way of plotting the solution is using a contour plot to plot the curves along which the solution is constant. It is very similar to what we did in Lecture a5.
set view map
unset surface
set contour
set cntrparam levels 30
unset key
set xlabel 't_n'
set ylabel 'x_k'
splot 'sol.txt' w l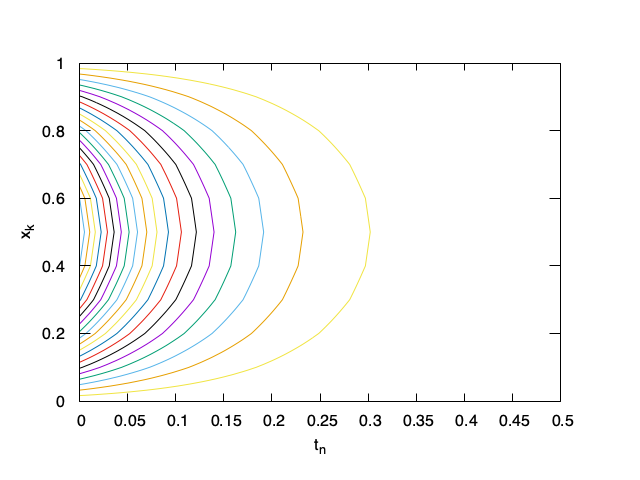
Exercise 1. Modify the Fortran code and solve the heat equation for each of the following data:
- u_0(x) = \sin(\pi x) + \sin(3\pi x), a = b = 0
- u_0(x) = x(1 - x) + x, a = 0, b = 1
- u_0(x) = \frac 12 - |x- \frac 12|, a = b = 0
Try also increasing M to 20 or decreasing it to 5 and see what happens.
Plot the numerical solutions in gnuplot.
Submit the plot for 3. with M = 10 to LMS with your student ID as the title.